基本理论

图 1.1

AlexNet是具有历史意义的一个网络结构，在此之前，深度学习已经沉寂了很久。2012 年，AlexNet在当年的ImageNet图像分类竞赛中，top-5错误率比上一年的冠军下降了十个百分点，而且远远超过当年的第二名。网络结构如图1.1所示，包含五层卷积层和三层全连接层，总共包含约6000万个参数。下面详细介绍AlexNet网络：

ReLU

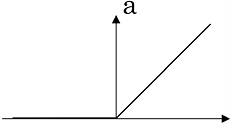
图 1.2

优点：

• 在输入大于 0 时候，不会出现梯度消失；
• 相较于 sigmoid 和 tanh 收敛速度大大提升，不含有 exp 运算，计算速度提升。

缺点：

• 输出不是关于中心点对称；
• 当输入小于 0，在前向传播时 ReLU 一直处于非激活状态，那么反向传播就会出现梯度消失(未激活的神经元局部梯度为 0 )，因此非激活的神经元无法进行反向传播，它的权重也不会更新；当输入大于 0 ，ReLU 神经元直接将梯度传给前面层网络；当输入为 0，梯度未定义，我们可以简单指定为 0 或 1（实际出现输入为 0 的概率很小）；
• 可能出现 ReLU 神经元失活问题，如 $max(0,w^{T}x+b)$ ，假设 $w、b$ 都初始化为 0，或者更新过程中，$w、b$ 更新为一种特别状态，使得 永远小于 0，那么该神经元权重将永远得不到更新。

Data Augmentation

神经网络是靠数据喂出来的，同时扩大数据集合可以有效地解决过拟合问题，可以通过一些简单的变换从已有的训练数据集中生成一些新的数据，来扩充训练数据集。

• 镜像对称（Mirroring）

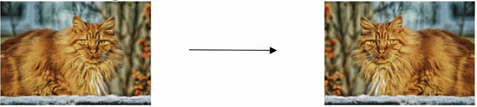
图 1.3

• 随机裁剪（Random Cropping）

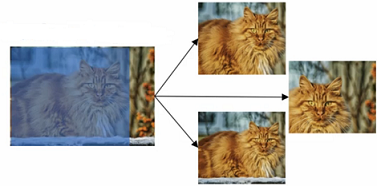
图 1.4

• 色彩变换（Color shifting）

在实践中增加的 RGB 值是根据某种概率分布来决定的。PCA 颜色增强，其含义是：比如图像呈现紫色，即主要含有红色和蓝色，绿色很少，那么 PCA 颜色增强就会对红色和蓝色增减很多，绿色变化相对少一点，所以使总体的颜色保持一致。

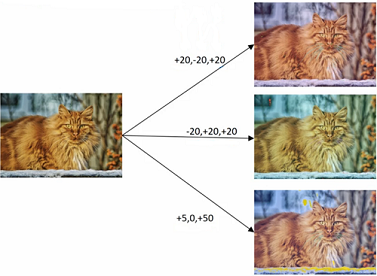
图 1.5

AlexNet Data Augmentation 做法是：

• Random Cropping：从 $256\times256$ 的图像中随机裁剪 $224\times224$（包括 Mirroring 图像），相当于将样本增加 $(256-224)^{2}\times2=2048$；
• Color shifting：采用 PCA 方法处理整个 ImageNet 数据集合，将每个素的 RGB 值 $\left[ I^{R}_{xy},I^{G}_{xy},I^{B}_{xy}\right]^{T}$ 加上 $\left[p_{1},p_{2},p_{3}\right]\left[ \alpha_{1}\lambda_{1},\alpha_{2}\lambda_{2},\alpha_{3}\lambda_{3}\right]^{T}$ 其中 $p_{i}$ 和 $\lambda_{i}$ 分别是 RGB 值的 $3 \times 3$ 协方差矩阵的第 $i$ 个特征向量和特征值。$\alpha_{i}$ 是一个服从均值为 $0$，标准差为 $1$ 的高斯分布的高斯变量。简单说明下怎么求解协方差矩阵的，假设训练集有 $m$ 张图片，每张图片大小为 $w \times h$，我们将 $m$ 图片转化为 $X \in R^{\left(m \times w \times h,3\right)}$ 的二维向量，三列分别表示 RGB 三个通道灰度值，对这个二维矩阵求协方差矩阵，可以得到 $3 \times 3$ 的 RGB 协方差矩阵 $C$，协方差具体求法如下公式(1.1)，其中 $x_{i}$ 表示第 $i$ 列的向量， $x_{j}$ 表示第 $j$ 列的向量。

$\left[ \begin{matrix} cov(x_{1},x_{1}) & cov(x_{1},x_{2}) & cov(x_{1},x_{3}) \\ cov(x_{2},x_{1}) & cov(x_{2},x_{2}) & cov(x_{2},x_{3}) \\ cov(x_{3},x_{1}) & cov(x_{3},x_{2}) & cov(x_{3},x_{3}) \end{matrix} \right] \tag{1.1} \\ $ 其中 $cov(x_{i},x_{j}) = E\left[\left( x_{i} - E\left[ x_{i}\right] \right) \left( x_{j} - E\left[ x_{j}\right] \right)^{T} \right]$

Dropout

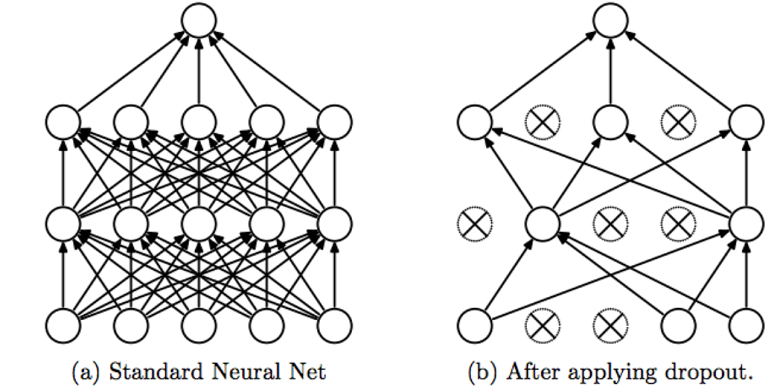
图 1.6

如图1.6所示，对第 $i$ 层进行 Dropout，保留某个神经元的概率为 keep_prob 。前向传播的时候让某个神经元的激活值以一定概率 1 - keep_prob 停止工作（即把该神经元的激活值设为0），为了不影响整个网络输出的期望值，未被Dropout的神经元的激活值除以 keep_prob，具体见算法1.1：

Train:
    d[i] = np.random.rand(a[i].shape[0],a[i].shape[1]) < keep_prob
    a[i] = np.multiple(a[i],d[i])
    a[i] /= keep_prob
    z[i+1] = w[i+1]a[i]+b[i+1]
Test:
    Do Nothing

为什么需要除以 keep_prob？假设 $l$ 层有 $50$ 个 uinits，keep_prob = 0.8，大概有 $10$ 个 uinits 被置 $0$，$z^\left[ l+1 \right] = w^\left[ l+1 \right] a^\left[ l \right] + b^\left[ l \right]$，$a^{\left[ l \right]}$ 的期望相比 Dropout 之前减少 20%，为了不影响 $z^{\left[ l+1 \right]}$ 的期望，$a^{\left[ l \right]}$ 需要除以 $0.8$ 用来修正或弥补 Dropout 掉的 20%。目的是确保即使在测试阶段不执行 Dropout 来调整数值范围，激活函数的预测结果也不会发生变化。（测试阶段不进行Dropout，因为如果在测试阶段应用Dropout，每次Dropout的神经元都是变化的，预测会受到干扰。） 为什么Dropout可以起到正则化作用？由前面可知正则化的本质是减少网络对某些神经元过分依赖。直观地认识，训练一个网络，每次迭代过程中，任何一个神经元都有可能被Dropout，所以后一层的神经元输入不会过分依赖前一层的任何一个神经元的输出，不会给前一层任何一个神经元太多权重，而是尽可能的均分到每个神经元上。和前面介绍的L2范数有异曲同工之妙。Cannot rely on any one feature,so have to spread out weights。

局部归一化

其中 $a^{i}_{x,y}$ 表示第 $i$ 个卷积核在 $(x,y)$ 位置产生的值再应用 ReLU 激活函数后的结果，$n$ 表示相邻的几个卷积核，$N$ 表示这一层总的卷积核数量，$k=2,n=5,\alpha=0.0001,\beta=0.75$ 是超参数。如图 1.7 所示，选取一个位置，在第三维度上穿过，图中白色区域，可以得到10个相邻的元素，然后利用公式(1.2)进行归一化。后面研究发现LRN作用不大，所以后面看到的网络一般不采用LRN。

图 1.7

模型分析

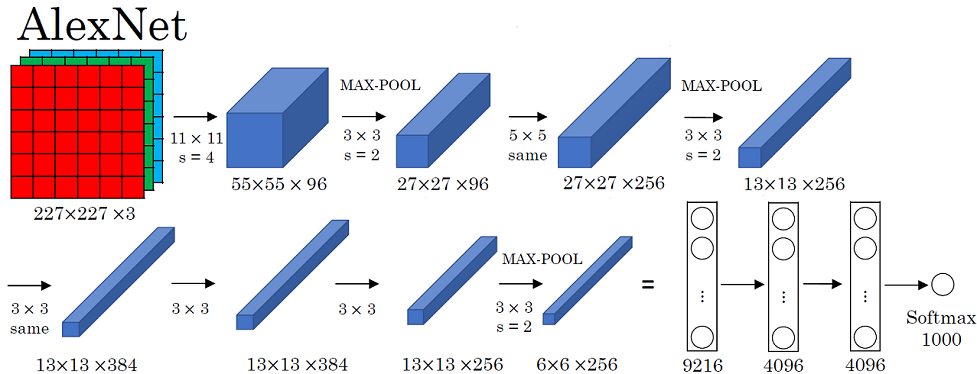
图 2.1

第一层 卷积层

• conv：输入的 $shape$ 为 $227\times227\times3$，$96$ 个 $11\times11$ 的卷积核，步长为 $s=4$，$Valid$ 方式。输出的 $shape$ 为 $55\times55\times96$，其中$\left\lfloor\frac{227-11}{4}+1\right\rfloor=55$ 。
• lrn：对卷积结果进行局部归一化。
• max-pool：输入的 $shape$ 为 $55\times55\times96$，池化参数 $f=3,s=2$，$Valid$ 方式，输出的 $shape$ 为 $27\times27\times96$，其中$\left\lfloor\frac{55-3}{2}+1\right\rfloor=27$

第二层 卷积层

• conv：输入的 $shape$ 为 $27\times27\times96$，$256$ 个 $5\times5$ 的卷积核，步长为 $s=1$，$Same$ 方式。输出的 $shape$ 为 $27\times27\times256$，其中 $padding：\frac{5-1}{2}=2$，$\left\lfloor\frac{27+2\times2-5}{1}+1\right\rfloor=27$。
• lrn：对卷积结果进行局部归一化。
• max-pool：输入的 $shape$ 为 $27\times27\times256$，池化参数 $f=3,s=2$，$Valid$ 方式，输出的 $shape$ 为 $13\times13\times256$，其中$\left\lfloor\frac{27-3}{2}+1\right\rfloor=13$

第三层 卷积层

• conv：输入的 $shape$ 为 $13\times13\times256$，$384$ 个 $3\times3$ 的卷积核，步长为 $s=1$，$Same$ 方式。输出的 $shape$ 为 $13\times13\times384$，其中 $padding：\frac{3-1}{2}=1$，$\left\lfloor\frac{13+2\times1-3}{1}+1\right\rfloor=13$。

第四层 卷积层

• conv：输入的 $shape$ 为 $13\times13\times384$，$384$ 个 $3\times3$ 的卷积核，步长为 $s=1$，$Same$ 方式。输出的 $shape$ 为 $13\times13\times384$，其中 $padding：\frac{3-1}{2}=1$，$\left\lfloor\frac{13+2\times1-3}{1}+1\right\rfloor=13$。

第五层 卷积层

• conv：输入的 $shape$ 为 $13\times13\times384$，$256$ 个 $3\times3$ 的卷积核，步长为 $s=1$，$Same$ 方式。输出的 $shape$ 为 $13\times13\times256$，其中 $padding：\frac{3-1}{2}=1$，$\left\lfloor\frac{13+2\times1-3}{1}+1\right\rfloor=13$。
• max-pool：输入的 $shape$ 为 $13\times13\times256$，池化参数 $f=3,s=2$，$Valid$ 方式，输出的 $shape$ 为 $6\times6\times256$，其中$\left\lfloor\frac{13-3}{2}+1\right\rfloor=6$

第六层 全连接层

• fc：$6\times6\times256\rightarrow4096$。
• Dropout：0.5。

第七层 全连接层

• fc：$4096\rightarrow4096$。
• Dropout：0.5。

第八层 全连接层

• fc：$4096\rightarrow1000$。

代码分析

相关代码放在 github 上，大家可以移步 github 下载，分以下几部分：

• generate_alexnet.py：训练数据；
• alexnet.py：AlexNet 模型；
• train_alexnet.py：训练 AlexNet 模型；
• predict_alexnet.py：验证 AlexNet 模型。

训练数据

采用 Kaggle Dogs vs. Cats Redux Competition 作为训练数据，在已经训练好的 AlexNet 模型上进行迁移学习，只训练后面三层的全连接层，对猫、狗进行分类。我把训练数据上传到腾讯云cos上，可以下载 train.zip，根据图片的文件名，可以对狗、猫的图片进行标注 cat:0, dog:1，数据分为训练集和验证集（85/15)，并分别保存在 train.txt 和 val.txt，格式为 filename label。 下面开始我们的数据处理吧。

mkdir data
cd data
wget http://tensorflow-1253902462.cosgz.myqcloud.com/alexnet/train.zip
unzip -q train.zip
cd ..
python
from generate_alexnet import ImageDataGenerator
ImageDataGenerator.get_image_path_label()

按照上面一步一步执行完，会生成 train.txt 和 val.txt，文件内容如下面所示：

data/train/dog.7412.jpg 1                               
data/train/cat.1290.jpg 0

训练 AlexNet 模型

模型结构具体细节可以参考第二部分的 模型分析 。我们在已经训练好的 AlexNet 上进行迁移学习，具体做法：前五层卷积层的权重和偏置不进行训练，直接赋值 toronto 大学已经训练好的参数 bvlc_alexnet.npy，后面三层全连接随机初始化，然后进行训练。原始的 AlexNet 是针对 $1000$ 个分类，最后一层的 $softmax$ 输出 $1000$ 个类别，我们这里仅仅对猫、狗进行分类，所以 $softmax$ 输出 $2$ 个类别。同样我把 bvlc_alexnet.npy 上传到腾讯云 cos 上，方便大家下载。 下面开始我们的模型训练吧。

wget http://tensorflow-1253902462.cosgz.myqcloud.com/alexnet/bvlc_alexnet.npy
nohup python train_alexnet.py &
tail -f train_alexnet.log

大概训练一个多小时，在验证集上准确率达到 97%，所以把训练过程写到 train_alexnet.log 文件中，nohup 可以防止进程被 SIGHUP 信号干掉。另外每训练完一个 epoch，会保存一次训练结果，如果中途中断训练，重新开始训练先读取上次训练结果，可以有效地防止从头开始训练。打开你的机器 9090 端口，可以通过 $tensorboard$ 查看训练的动态过程,如图 3.1和图 3.2 所示，分别是训练集上的准确度和损失函数。

tensorboard --port 9090 --logdir=/home/ubuntu/machinelearning/alexnet/train_alexnet
http://IP:9090/

下面可以喝杯茶耐心地等待训练过程啦，当然如果你不想等待训练过程，我这里也提供已经训练好的模型，放在腾讯云 cos 上，大家可以下载 AlexNet_Dogs_Cats_model.zip。

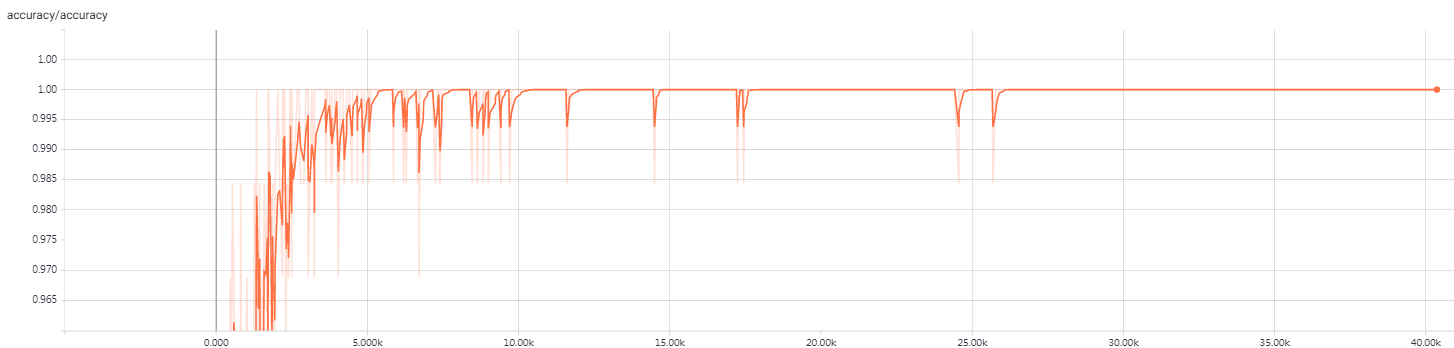
图 3.1

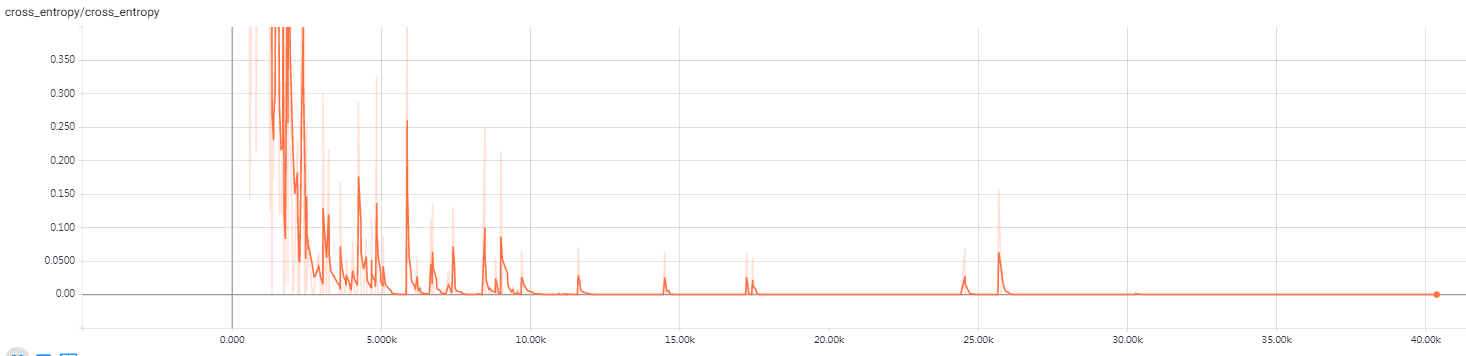
图 3.2

验证 AlexNet 模型

主要实现两个功能：

ImageNet 图像分类

直接读取 bvlc_alexnet.npy 的权重，我自己随便在 Google 上下载三张图片放在腾讯云 cos 上，大家可以下载或者自己去百度下载图片。 下面开始我们的图片分类，取概率最大的top5

wget http://tensorflow-1253902462.cosgz.myqcloud.com/alexnet/Elephant.jpg
wget http://tensorflow-1253902462.cosgz.myqcloud.com/alexnet/cat.jpg 
wget http://tensorflow-1253902462.cosgz.myqcloud.com/alexnet/dog.jpg

python predict_alexnet.py 1 Elephant.jpg
输出：
  African elephant, Loxodonta africana 0.692875 
  tusker 0.280027
  Indian elephant, Elephas maximus 0.0270912
  Arabian camel, dromedary, Camelus dromedarius 5.40385e-06
  sorrel 5.34084e-07

当然你也可以试试对 cat.jpg、dog.jpg 分类，看看结果。

Cats vs. Dogs 分类

仅仅对猫、狗分类，所以我们只能使用 cat.jpg、dog.jpg 图片。

python predict_alexnet.py 2 cat.jpg
输出：
  cat

python predict_alexnet.py 2 dog.jpg
输出：
  dog

参考

ImageNet Classification with Deep Convolutional Neural Networks

AlexNet implementation + weights in TensorFlow

DeepLearning.ai

Finetuning AlexNet with TensorFlow